1 导论

　　 权衡论证(pro and con arguments)是一种同时包含正面的、支持结论的理由(pros)与反面的、反对结论的理由(cons)的论证，其结论的证成(至少在论证者看来)源于正面理由的逻辑力量经过权衡胜过了反面理由。1971年，美国伦理学家韦尔曼(Carl Wellman)在《挑战与回应：伦理学中的证成》[29]一书中首次明确论及了这一独特论证的存在，他称其为“联导论证”(conductive argument)①的第三种模式。②自1980年以来，非形式逻辑学家戈维尔、希契柯克、汉森(Hans V.Hansen)、弗里曼等先后针对权衡论证的结构与图解提出了各自的观点和方法，但彼此之间在如下三个问题上意见分歧严重：

　　 i)如何看待反面理由(counter-consideration)③在论证中的地位？

　　 ii)如何把握正面理由、反面理由与结论这三者之间的联系方式？

　　 iii)如何直观地图解权衡论证的结构？本文将通过揭示上述学者在这些问题上的所见所蔽，对权衡论证的结构与图解作进一步的研究，一方面提出处理反面理由之地位问题的具体方案，从宏观与微观两个层面把握权衡论证的结构，引进一种新的方法来图解其结构，另一方面对我2010年的工作([20])进行必要的修正与补充。

　　 2 韦尔曼论权衡论证

　　 “权衡论证”与韦尔曼所说的“联导的第三种模式”(the third pattern of conduction)二名一实，后者最明显的特征是“结论同时从正面理由与反面理由中得出(some conclusion is drawn from both positive and negative considerations)。”([29]，第57页)例如：例1 尽管你家草坪需要修剪，你还是应该带你儿子去看电影，因为那部电影非常适合小孩，而且明天就要下线了。([29]，第57页)④

　　 这里，“你应该带你儿子去看电影”是结论，“那部电影非常适合小孩”与“那部电影明天就要下线了”是为结论提供支持的正面理由，由“尽管”引导的“你家草坪需要修剪”则是反对结论的理由。在证成结论的过程中，论证者除了承认有支持结论的理由，也承认存在反对结论的理由，但通过对正、反两组理由的逻辑力量的权衡(weighing)，最终认为正面理由胜过了反面理由，结论得以证成。

　　 按照逻辑学中通行的定义，论证指的是一组命题，其中的一个或多个命题被认为为另一个命题的真实性或可接受性提供了支持。从构成要素的角度看，论证总是可以区分出两个组成部分：前提和结论，前提为结论的真实性或可接受性提供支持，结论的真实性或可接受性以前提为基础([5]，第6页；[19]，第1页)。由于正、反两面的理由同时出现于权衡论证中，随之而来的一个问题就是：如何看待反面理由在论证中的地位？按韦尔曼的理解，任何论证均由前提、结论和一个隐含的对于有效性的宣称(an implicit claim to validity)所构成。([29]，第102页)鉴于后者更多地与论证评估相关，因此从分析或描述的角度看，论证的构成要素实际上就是前提和结论。就此而言，韦尔曼的理解与通行说法是一致的。不过，他并不认为反面理由是构成论证的、既非前提亦非结论的第三个要素，因为根据他对“前提”的定义——“前提是或被认为是任何支持或反对结论的理由”([29]，第90页)，反面理由也是前提。不难看出，韦尔曼改变了“前提”一词的通常含义，扩大了其外延。相应地，他对反面理由地位的判定——反面理由是前提——虽与他本人对“前提”的定义以及对论证要素的说明保持了一致，但却与“前提”一词的通常含义相矛盾，因为前提一般被视作在论证中为结论提供支持的部分，即仅仅对应于韦尔曼所说的正面理由。

　　 此外，一个关乎权衡论证结构的关键问题是：正、反两面的理由与结论是如何联系在一起的？韦尔曼本人并未论及这一问题，不过根据他对联导的第二种模式的描述，我们可以作些推测。在这一模式中，“若干个理由被联合起来置于一个统一的论证(a unified argument)之中，结论从它们得出，但每个理由都与结论独立地相关(independently relevant)。”([29]，第56页)例如：例2 你应该带你儿子去看电影，因为你允诺过这事儿，而且这是一部好电影，更何况今天下午你没有别的更好的事儿可做。([29]，第57页)

　　 相异于权衡论证，例2的前提仅仅陈述了支持结论的正面理由。对于此类论证的结构，有两点值得注意：首先，由于若干个理由分别地与结论相关，即其中一个理由如果被认为是假的或不可接受而被移走，并不影响剩下的理由与结论之间的相关性，因此这种论证实际上包含着不止一种彼此独立的支持关系；其次，结论得以证成的基础，不在于任何单个的理由，而是“证据的逻辑聚合”(the logical convergence of evidence)，即所有单个理由联合在一起为结论提供支持([29]，第57页)。

　　 在提及若干正面理由被用来支持结论后，韦尔曼补充道：“有可能还存在一些没有提及的、相关的理由，特别是在另外一边的(on the other side)。”([29]，第56页)设想这些处于“另外一边”的理由——反面理由——被补充进了一个第二种模式的联导中，这就意味着我们获得了一个类似例1的第三种模式的联导论证，即权衡论证。相异于在第二种模式中结论得自正面理由的逻辑聚合，论证者在此面临的是一个完全不同的问题——“如何估计正面与反面理由，支持与反对结论的理由的相对的逻辑力量(the relative logical force)。”([29]，第59页)这就是说，结论能否证成的关键，不是正面或反面理由的逻辑聚合，而是“相较于反对结论的理由，支持结论的理由具有多大的逻辑力量。”([29]，第68页)就此而言，在权衡论证中，每个单独的理由，无论是正面的还是反面的，是否还像在第二种模式中那样独立地与结论相关？就正、反理由的整体而言，它们究竟如何与结论联系在一起？如何用直观的方法来图解权衡论证的结构？很遗憾，相较于如何评估权衡论证的好坏，韦尔曼对这些关涉此类论证之结构的重要问题并未表现出多大的兴趣。

　　 3 反面理由在论证中的地位

　　 “权衡论证”、“反面理由”等概念的引入，对关于论证要素的通行见解提出了挑战。尽管韦尔曼对反面理由在论证中地位的说明可谓自圆其说，但与“前提”一词的通行含义却是冲突的。此后，希契柯克、戈维尔、汉森等人继续对这一问题给予了关注。

　　 在1983年出版的《批判性思维：信息评估指南》[16]中，希契柯克在考察所谓“平衡考虑论证”(balance-of-considerations argument)的时候触及了权衡论证的问题。在他看来，存在着如下一种论证结构：

　　 它包含若干个理由，每一个都对结论具有某种意义但彼此联合在一起(in conjunction with one another)可以为结论提供相较于任何单个理由所能提供的更多的支持。我们可以将这种论证结构称作独立的但彼此增强的理由支持同一个结论(independent but mutually enhancing reasons for a conclusion)。紧接着上述描述，他指出：“我们把所有此类论证——不管它们在前提中是否包含反面的因素(negative factors)——叫作平衡考虑论证。”([16]，第51-52页)很明显，平衡考虑论证似可分成两种，一种对应于韦尔曼所说的第二种模式的联导，其前提仅由正面理由构成；另一种对应于第三种模式的联导，其前提同时包含了支持与反对结论的理由。这就是说，权衡论证实质上是平衡考虑论证的一个子类。

　　 关于反面理由在论证中的地位，希契柯克的看法并不明确。从总体上看，他坚持通行的“前提”定义，认为前提的作用在于为结论的证成提供支持性的证据(supporting evidence)([16]，第31、34页)，而反面理由因其不能为结论提供支持，不属于前提的范围。不过，他有时又说平衡考虑论证可能“在其前提中包含反对结论的理由(include among their premises considerations against the conclusion)”([16]，第130页)，这似乎又把反面理由视作“前提”外延的一部分。

　　 戈维尔对权衡论证的讨论集中于她的专著《论证哲学》[11]与具有广泛影响的教材《论证的实践研究》[12]⑤之中。她把权衡论证视作一种典型的联导论证，而“联导论证的一个共同特征就是论证者可能承认事实上或看上去反对结论的理由。这些反面理由是与结论否定相关的(negatively relevant)陈述”([11]，第155页)。由于“在一个有说服力的(cogent)论证中，前提必须与结论肯定相关(positively relevant)”，因此“反面理由在论证中并不具有前提的地位”([12]，第355-356页)，戈维尔甚至提出可以把反面理由设想为是“反前提”(anti-premise)([11]，第156页)。将反面理由排除在前提之外，这一处理无疑与“前提”一词的通常含义保持了一致，但她在此并没有正面回答反面理由在论证中究竟处于何种地位。

　　 在《平衡考虑论证评注》一文中，汉森系统梳理和评论了关于反面理由地位的几种主要观点([14]，第35-40页)。在他看来：

　　 1)反面理由不是前提，因为根据通行的理解，前提只能是那些与结论肯定相关的、为结论提供支持的命题。

　　 2)反面理由不是背景知识(background knowledge)，因为反面理由明确为论证者所承认并且被清晰地表述在了论证之中。

　　 3)反面理由不是对结论的限定(qualifications about the conclusion)。在权衡论证中，结论得以证成的根据是正面理由的逻辑力量胜过了反面理由，由于正、反理由均参与了为证成结论而进行的权衡，因此与其说反面理由是对结论的限定，不如说是对得出结论的那个推理过程的限定。

　　 4)反面理由不是反论证的前提(the premises of a counter-argument)。相对于权衡论证的结论K，K的反面理由可以为K提供支持，从而成为以K为结论的反论证的前提。但是，这种处理的一个消极后果就是把作为一个同时包含正、反理由的统一论证分解为了彼此对立的两个论证。

　　 尽管对结论提出了挑战或反对，反面理由对于权衡论证无疑具有构成性的意义，因为一旦不包含反面理由而仅仅包含正面理由，权衡论证就将不再是权衡论证。那么，反面理由在论证中究竟具有何种地位呢？韦尔曼、希契柯克对此问题的回答均存在某种形式的不一致，戈维尔明确否认反面理由是前提，但与汉森一样，她也没有提供肯定的答案。我在([20]，第25页)中指出，鉴于反面理由明确为论证者所承认并且被清晰地表述在了权衡论证之中，因此我不赞成那种仅仅把反面理由视作背景知识的看法，也不赞成弗里曼所说的反面理由“不构成某种额外的论证要素的类型”(some additional category of argumentative element)([6]，第173-174页)。我认为在如何看待反面理由的地位这一问题上，如果我们把保持“论证”、“前提”在逻辑学中的通常含义置于优先考虑的位置，再加上前提与结论往往被视为构成论证的基本要素，那么可以把反面理由视作构成论证的一个独特的非基本的要素(a distinctive non-basic component)。⑥

　　 针对我([20]，第21页)和汉森([14]，第35-38页)的批评，戈维尔也强调不应像韦尔曼那样任意扩大“前提”的外延，将正、反两面理由均视为前提，而是可以在保持“前提”通常含义的同时，通过对论证要素作扩展的理解来回答反面理由的地位问题。在她看来，前提和结论是任何论证都不可或缺的基本要素，除此之外，论证还可能包含其他一些重要的但不是基本的要素，例如，反面理由、指示词(indicator word)等。就指示词而言，除了通常提及的那些标识前提或结论的语词，还应该包括引导反面理由的指示词，如“虽然”、“尽管”、“即使”等等。([13]，第269页)简言之，反面理由是论证的一个非基本的构成要素，它一般出现于权衡论证之中，与前提(正面理由)一道构成结论得以证成的基础。

　　 4 正面理由、反面理由与结论的联系方式

　　 把握权衡论证的结构，其关键就是如何看待正面理由、反面理由与结论这三者之间的联系方式。如前所述，韦尔曼并没有论及正、反理由与结论是如何联系起来的，而希契柯克似乎认为权衡论证，作为平衡考虑论证的一个子类，理所当然地具有平衡考虑论证的一般结构。但是，事实果真如此吗？⑦

　　 首先，希契柯克认为，“通过把每个单独的理由视作一个支持结论的论证(an argument supporting the conclusion)，我们就能够刻画出这些所谓平衡考虑论证的结构。”([16]，第51页)但是，权衡论证同时包含正、反两方面的理由，这一事实与他在此把平衡考虑论证的前提仅仅理解为正面理由是不一致的。进而言之，把权衡论证的理由都视作在支持结论也不合乎事实，因为有一些理由(反面理由)明显是在反对结论。

　　 其次，希契柯克认为，平衡考虑论证的每一个前提都独立地为结论提供了某种程度的支持，但权衡论证的情况并非如此。在正、反两组理由中，单个理由的确仍然独立地与结论相关，即单个的正面理由在正面理由组中为结论提供独立的支持，单个的反面理由在反面理由组中独立地对结论提出反对。但是，相互冲突的两组理由在整体上是否仍然是彼此独立的呢？要回答这一问题，让我们来看一个结构上最简单的权衡论证，即彼此矛盾的两组理由中都只包含一个理由。下面这个例子改写自韦尔曼([29]，第51页)：例3 鉴于①他含蓄的友善，我认为②他在道德上还是一个好人，尽管③他为人比较冒失。

　　 在这个论证中，正面理由①与反面理由③还是独立地与结论②相关吗？如果其中一个理由被认为不能成立，另一个与结论的相关性不会受到影响吗？既然一个论证必须同时包含正、反两组理由才成其为权衡论证，那么在例3中，如果①被移走，②就不可能从③得到证成，因为后者是反对而非支持②的；如果④被移走，②固然还可能从①得到证成，但例3在此时已不再是一个权衡论证。就此而言，①和③对于例3作为一个权衡论证、对于证成②来说，都是不可或缺的。推而广之，在所有权衡论证中，正面理由组与反面理由组——不论各自包含多少个单独的理由——对于这些论证之为权衡论证、对于结论之证成依赖于正、反两组理由之逻辑力量的权衡来说，都是不可或缺的。当然，这并不否认在各组理由中，单个的理由仍然独立地与结论相关。

　　 最后，希契柯克认为在平衡考虑论证中，所有前提联合在一起能够为结论提供相较于任何单个前提所能提供的更强支持，但这在权衡论证中也不是事实。对反面理由组来说，所有单个理由的联合所能提供给结论的不是更强的支持，而是更强的反对。论证者在权衡时更为关注的不是对结论而言是否存在“彼此增强的理由”或者“累计的支持”(cumulative support)，而是是否“正面理由胜过了(outweigh)反面理由”，“是否支持结论的因素胜过了那些反对结论的因素”。([16]，第51、130页)

　　 综上所述，尽管希契柯克把权衡论证视作平衡考虑论证的一个子类，但他对于平衡考虑论证一般结构的理解其实并不适合用来把握正、反理由与结论究竟是如何联系在一起的。

　　 与希契柯克一样，戈维尔在[11，12]中也没有直接讨论权衡论证的结构。在她看来，联导论证的一个共同特征就是论证者可能承认反面理由，由此我们可以很自然地推定她关于联导论证一般结构的见解也适用于权衡论证，但下文将证明这种推定是不能成立的。

　　 戈维尔指出，“在拥有若干前提的联导论证中，这些前提以收敛地方式(convergently)支持或者被提出来支持结论。”([11]，第156页)那么，收敛支持是怎样一种支持关系呢？

　　 在这种支持中，前提联合起来(work together)以一种累计的方式支持结论，但并不是组合在一起(linked)。如果其他前提被移走了，一个前提对于结论的意义将不受影响：但是，当把前提联合起来予以考虑时，论证将得到加强，因为此时提供了更多的证据。([12]，第55页)据戈维尔的用词法，收敛支持与收敛结构(convergent structure)是同一个东西。不难发现，韦尔曼所说的联导的第二种模式、希契柯克所说的平衡考虑论证的结构，以及戈维尔这里所说的联导论证的收敛支持，其实质都是在说这些论证的前提与结论之间具有一种收敛结构。

　　 接下来，我将用三点理由证明戈维尔对联导论证的结构——收敛支持——的描述也不适合用来把握权衡论证中正、反理由与结论的联系方式。

　　 首先，收敛支持不能容纳反面理由。根据戈维尔的定义，在收敛支持中，前提(正面理由)以一种累计的方式支持结论，这意味着这种支持关系仅仅存在于正面理由与结论之间，在收敛支持中没有反面理由存在的可能性。

　　 其次，理由对于结论的独立相关性不能完全适用于对权衡论证的结构的刻画。权衡论证包含两组相互冲突的理由，尽管单个理由在所属的理由组中仍然独立地与结论相关，但正、反两组理由作为整体彼此独立地与结论相关却不是事实。这就意味着这两组理由必须组合在一起才能使一个论证成为权衡论证，一旦其中一组被移走，该论证就将不再是一个权衡论证。

　　 最后，收敛支持未能反映结论是如何从正、反两面的理由中得到证成的。对于正面理由来说，收敛支持的确能够为结论提供相较于任何单个理由所能提供的更多累计的支持，但在权衡论证中，为了证成结论，论证者不仅要考虑正面理由组为结论提供了多强的支持以及反面理由组在多大程度上对结论提出了反对，更为重要的是，还要考虑前者是否在逻辑力量上胜过了后者。很明显，收敛支持是无法反映这种正、反理由之间的比较与权衡的。

　　 既然希契柯克、戈维尔所主张的收敛支持并不适合用来刻画正、反理由与结论之间的联系方式，那么究竟该如何正确把握权衡论证的结构呢？在我看来，权衡论证具有一种混合结构(a hybrid structure)，它可以分为两层，分别对应着关于权衡论证的两个基本事实：其一是所有权衡论证均包含着两组相互冲突的理由，其二是每组理由中都包含着一个或多个分别与结论独立相关的理由。下面，我用PC表示正面理由组，CC表示反面理由组，K为结论。

　　 针对第一个基本事实，我认为就宏观层面上的PC、CC和K之间的联系而言，权衡论证包含着一个组合结构(linked structure)。据非形式逻辑的论证结构理论，相异于收敛结构，组合结构要求前提必须组合在一起才能为结论提供支持，移走一个前提将对剩余前提对结论的意义产生影响，所有前提对于结论的证成来说都是不可或缺的。从前文对例3的分析可知，必须至少同时包含一个正面理由和一个反面理由，一个论证才能成其为权衡论证。推而广之，一个论证要成其为权衡论证，必须同时包含PC和CC；论证者在权衡论证中要证成K，必须同时将PC和CC纳入权衡过程，二者对于K的证成缺一不可。这就是说，在PC、CC和K之间存在着一个组合结构。

　　 针对第二个基本事实，我认为就微观层面上的PC、CC中的单个理由与K之间的联系而言，权衡论证又包含着一个收敛结构。戈维尔曾分析过如下这个例子：例4 我想①比尔生气了，因为②当他看见我时他显得有些紧张，而且③他再也没有像往常那样请我喝咖啡。虽然④他还是跟我打招呼，⑤我们一起工作时也算有效率，但⑥他看起来应该是生气了。([12]，第355页)

　　 在这个论证中，PC包含两个理由(②和③)，CC包含两个理由(④和⑤)，结论K表述了两次(①和⑥)。在PC中，②和③为K提供了独立的支持，其中一个被移走，不会影响到剩下那个与K的相关性，这就是说，②和③对K给予了收敛的支持。在CC中，④和⑤各自独立地对K提出了反对，如果其中一个被移走，也不会影响到剩下那个与K的相关性，这就是说，④和⑤与K之间也存在着一种收敛结构。⑧相异于戈维尔等人将“收敛结构”与“收敛支持”等而视之，这里所说的收敛结构既适用于若干个正面理由独立地支持同一个结论，也适用于若干个反面理由各自独立地反对同一个结论，也就是说，既可指收敛支持，也可指收敛反对。

　　 要言之，权衡论证具有一种由收敛与组合混合而成的双层结构，其中收敛结构存在于微观层面上单个的正、反理由与结论之间，组合结构则存在于宏观层面上作为整体的正、反两组理由与结论之间。⑨

　　 5 权衡论证结构的图解

　　 在明确了权衡论证的结构之后，进一步的问题就是如何用直观的方法对论证进行图解。在我看来，论证图解(argument diagramming)具有双重目的：其一是从分析或描述的角度来回答“这是一个什么样的论证”，为此在图解时要尽可能地显示它的前提、结论和可能存在的其他构成要素，以及这些要素是如何联系起来的；其二是着眼于评估，通过直观地显示论证的结构来为回答“这是否是一个好论证”创造条件，为此对论证的要素及其相互关系的直观显示就应该有助于判定结论是否从前提得到证成。

　　 韦尔曼没有考察权衡论证的结构，当然也就不可能讨论如何图解的问题。希契柯克在[16]中引进了一种图解方法，其基本思想是在正面理由前加“+”，反面理由前加“-”，然后将所有理由总括起来支持结论。下面，我对他自己所举的一个例子稍加修改用以具体说明这种方法：例5 ①我们必须避免建造核电站，因为②核反应堆堆芯的熔毁可能引发灾难性的后果，而且③目前尚无成熟的方法来安全处置放射性废料，尽管④不存在核电站爆炸的危险，⑤它们也不会加剧全球变暖。([16]，第132页)

　　 这个论证共计包含两组4个不同的理由，其中由“因为”引入的②和③是正面理由，分别独立地支持结论①；由“尽管”引入的④和⑤是反面理由，各自独立地反对结论。按照上面介绍的方法，例5的结构可图解如图1：⑩

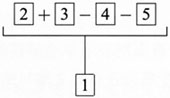
　　 着眼于对论证要素及其联系方式的显示，希契柯克的方法至少有三个优点。第一，借助“+”、“-”，它很好地显示了这种论证同时包含着正、反两面的理由；第二，通过将所有理由括起来，它在一定程度地显示了正、反理由对于结论的证成是不可或缺的，即权衡论证在宏观层面上包含着一个组合结构；第三，由于“+”、“-”也象征着计算，它也较好地显示了结论的证成来自于对正、反理由的比较和权衡。但是，这种图解也存在一定的缺陷，例如，没有用线段将表示单个理由的数字方框与结论方框联系起来以表示独立的支持或反对，因此未能显示出权衡论证在微观层面上所包含的收敛结构。又如，对论证要素及其相互关系的图解应有助于评估结论是否从前提得到证成，而在权衡论证中，结论得以证成的根据在于正面理由的逻辑力量经过权衡胜过了反面理由，但在希契柯克的图解中，仅仅借助“+”、“-”并不能明确显示上述权衡的结果。

　　 戈维尔在[12]中引进的图解在某些方面克服了希契柯克方法的不足，这一图解的基础是对收敛支持的图解。首先来看她本人分析的一个论证实例：例6 ①在人群中，她的视线须臾也没有离开过他，而且②当他出城后，她总是寝食难安。③在聊天中，只要有机会，她就会提到他的名字。④还没有哪位男士如此长时间地引起她的关注。显然⑤她爱上他了。([12]，第352页)

　　 这个论证的每个前提都独立地与结论肯定相关，因此其结构——收敛支持——可图解为图2：

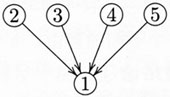
　　 图2用指向结论的直线箭头把表示单个前提的数字圆圈与结论圆圈直接联系起来，很好地显示了单个前提各自独立地与结论相关。在此基础上，我用前述例4来说明戈维尔如何图解权衡论证的结构。在那个论证中，①是结论，②和③是正面理由，④和⑤是反面理由。与用直线箭头来显示单个正面理由对结论的支持不同，戈维尔用波浪箭头来显示单个反面理由对结论的反对。这样，例4的结构就可以图解为图3。(11)

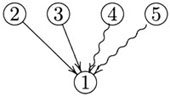
　　 相较于希契柯克的方法，戈维尔图解的一个明显优点就是它可以直观地显示单个理由如何独立地与结论相关，即能够很好地显示权衡论证在微观层面上所包含的收敛结构。例如，在图3中，通过②、③与①之间的直线箭头可以很容易读出前者分别地与后者肯定相关，而借助④、⑤和①之间的波浪箭头则能够读出前者分别地与后者否定相关。不过，这一图解也存在着两点较为明显的缺陷：第一，它不能很好地显示权衡论证在宏观层面上的组合结构，即作为整体的正、反两组理由对于结论的证成是不可或缺的；第二，它没有明确表达结论的证成(至少在论证者本人看来)源于正面理由的逻辑力量经过权衡胜过了反面理由。

　　 针对汉森([14]，第38-42页)和我([20]，第22-24页)对其图解缺陷的批评，戈维尔后来在([13]，第270-275页)中对上述图解进行了修正。她承认权衡论证具有一种由收敛和组合混合而成的双层结构，但为了尽可能充分地显示这一结构，她对权衡论证的总体特征进行了重新表述：

　　 有理由接受K，尽管(although)也有理由不接受K，不过(nevertheless)支持的理由胜过了反面理由，因此(therefore)接受K是合理的。([13]，第274页)这里，支持的理由胜过了反面理由构成了权衡论证的结论得以证成的根据。关于这一根据，戈维尔进一步解释道：

　　 如果我们认为一个联导论证是有说服力的，我们就必须坚持这样一个判断——前提中的理由合计起来为结论提供了好的理由——哪怕是对比那些反对结论的反面理由。这就是说，我们坚持这样一个判断——平衡考虑之后(on balance)，正面理由胜过了反面理由。([11]，第170页)受到汉森([14]，第39-40页)的影响，她把“正面理由胜过反面理由”这个判断称为“平衡考虑的前提”(on-balance premise，以下简称“OBP”)，并且把权衡论证在宏观层面上的组合结构理解为存在于PC、CC、OBP与K之间。(12)

　　 在上述工作的基础上，戈维尔给出了一种权衡论证的新图解(图4)：

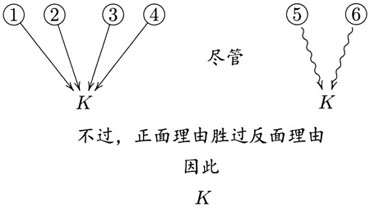
　　 按她自己的解释，这一图解虽谈不上完美，但至少部分地克服了原有图解存在的缺陷。例如，能够继续显示单个的正、反理由与结论之间的收敛结构，而PC、CC、OBP与K之间的联系——宏观层面上的组合结构——则可以通过“尽管”、“不过”这些表示合取(conjunction)的自然语言连词表达出来。此外，图4以文字形式表达了OBP这一结论得以证成的根据，也为评估论证创造了条件。不过，我认为戈维尔的这种新图解仍有值得商榷的地方：

　　 第一，这一图解更多地是从过程(process)角度来显示论证者如何从正、反理由得出结论的推理过程，而不是从结果(product)的角度来显示权衡论证的构成要素及其相互联系。从戈维尔对权衡论证总体特征的重新表述以及她在具体分析时更青睐于使用“阶段”(stage)而非“level”(层面)不难发现，结果视角已被过程视角所取代。(13)

　　 第二，与对过程视角的强调相关，新图解中出现了三个表示同一结论的符号K，这与权衡论证只有一个结论的事实明显不相吻合。之所以出现这种情况，一个重要原因就是戈维尔在新图解中更多显示的是论证者得出结论的那个推理与权衡的过程，而不是作为该推理、权衡过程之结果的那个论证。

　　 第三，在这个图解中，符号与文字混用，这明显与戈维尔在图解其他类型的论证时的做法不一致；而且引入文字主要是为了显示权衡论证在宏观层面上的组合结构，这又使得这一图解具有一种明显的特设(ad hoc)的性质。

　　 第四，戈维尔将OBP显示于图解之中，的确有助于评估结论是否从前提得到证成，但存在的问题有二：其一，在以自然语言为载体的权衡论证中，所谓OBP往往是隐含的(implicit)，并没有明确表达在作为结果的论证之中，这一点也为戈维尔本人所承认；其二，对结论的证成来说，“正面理由胜过反面理由”这个判断是在元层次(a meta level)上起着类似图尔敏所谓担保(warrant)([27]，第91页)的作用，即为从正、反两面的理由过渡到结论发放许可，或者说，为从PP、CC过渡到K提供证成。因此，不能把它视作权衡论证的前提或省略前提，它也不应该出现在PC、CC和K的组合结构之中。鉴于此，下文我将这一判断称作“平衡考虑的理由”(on-balance consideration，简称“OBC”)。

　　 与戈维尔的新图解类似，汉森([14]，第40页)在其图解中也试图显示权衡论证所包含的组合结构，但存在的主要问题是把“正面理由胜过反面理由”视作前提，并将其与正面理由置于一个组合结构中，排除了反面理由本身在组合结构的地位；同时未能显示出权衡论证在微观层面上的收敛结构，根本抹掉了单个理由各自对于结论的相关性。见图5：

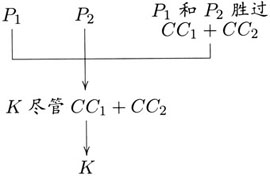
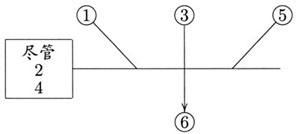
　　 此外，弗里曼在([8]，第140页)中也提出了一种图解权衡论证的方法。见图6：

　　 这一图解在一定程度上既显示了正面理由①、③和⑤各自独立地为结论⑥提供支持，又通过水平线显示了这些理由联合起来为结论提供了更强的支持；反面理由②和④则被置于水平线左端的方框内。弗里曼的图解是以顺时针旋转90°的图尔敏模式为基础的，但它未能显示单个反面理由各自对于结论的相关性，也没有很好地表达存在于正、反理由和结论之间的组合结构。此外，着眼于为评估论证创造条件，这一图解也未能显示出结论得以证成的根据。

　　 在我看来，对戈维尔在[12]中提出的旧图解稍加完善，就可以更为充分地显示权衡论证的结构。所谓更充分，就是说一方面它在很大程度上能完整显示权衡论证的双层结构，另一方面能显示结论得以证成的根据，即OBC。而要做到这两点，必须首先把OBC表达在图解中。一般而言，在图解论证结构时，并不需要显示论证者在证成结论时所使用的担保，即允许从前提过渡到结论的那个或那些推理规则、理论原理、经验概括等等，因为这个担保根本不是前提或省略前提。但是，在权衡论证中起着类似担保功能的OBC或许是个例外，将其显示出来将有助于更为充分地对权衡论证进行图解。

　　 受到希契柯克的启发([16]，第60页)，我认为可以在图解权衡论证时引入下面一个构件来表达OBC：

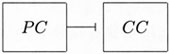
　　 这里，OBC(“正面理由胜过反面理由”)被直观地表达为PC“推倒”CC。如果将这个构件整合进戈维尔原来的那种图解，权衡论证的结构就可以得更为充分的显示。

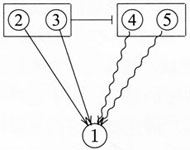
　　 首先，来看前述例4。按戈维尔的旧方法，这个论证可以图解为图3。结论①得以证成的根据即OBC在这个例子中具体表现为“正面理由②和③的逻辑力量胜过反面理由④和⑤”。将图3和图4加以重合，移出后者中的“PC”和“CC”，再将相应的空白方框分别框住②和③、④和⑤，这样例4的结构就可图解为图8：

　　 图8清晰地显示了这个论证包含着两个独立支持结论的正面理由(②和③)，以及两个分别对结论提出反对的反面理由(④和⑤)。由于从图中可以准确读出②和③联合起来对①的支持胜过了④和⑤在总体上对①的反对，这说明尽管意识到反面理由的存在，但经过正、反理由的权衡，论证者依然主张①。

　　 其次，如前所述，正、反两组理由都有可能只包含一个理由，这样存在于若干个单个理由与结论之间的收敛结构就不复存在。这种情况的权衡论证也可以通过图9或图10来进行图解。例如，图9就显示了例3所代表的最简单的权衡论证的结构。由于例3仅仅包含一个正面理由①和一个反面理由③，因此没有必要再用方框将这些理由分别框住，于是OBC就可以直接图解为①“推倒”③。

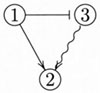
　　 图10则显示这个权衡论证包含两个正面理由(②和③)和一个反面理由(④)，因此需要一个方框来框住②和③。这样，OBC就可图解为②和③联合在一起“推倒”④：

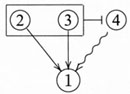
　　 图10

　　 不难发现，我提出的图解权衡论证的方法比戈维尔的旧图解多了一个构件，即OBC所代表的PC“推倒”CC。在我看来，正是借助这一构件，PC、CC对于K之证成的不可或缺，或者说，宏观层面上PC、CC与K之间的组合结构，可以得到某种程度的显示。由于这种图解保留了单个理由与结论之间的直线箭头和波浪箭头，因此微观层面上存在于若干个理由与结论之间的收敛结构也得到了显示。不止于此，PC“推倒”CC这一构件的引入，也清晰地显示了权衡论证的结论得以证成的根据，从而为评估论证创造了条件。对后面这一点，下文再稍作展开。

　　 如前所述，对一个论证进行图解，不仅是为了通过显示该论证的要素及其相互联系来回答“这是一个什么样的论证”，还应通过图解来为回答“这是否是一个好论证”创造条件，即着眼于判定结论是否从前提得到证成来进行图解。就评估权衡论证的好坏而言，除了要评估正、反理由的真实性或可接受性，还要评估它们与结论的相关性，更为关键的是要评估OBC的真实性，即正面理由的逻辑力量是否真的胜过了反面理由。希契柯克、弗里曼的图解以及戈维尔的旧方法等都未能在图形中显示OBC，因此很难说这些图解为评估论证创造了条件，而我所建议的图解则在很大程度上避免了这一问题。进而言之，评估者在评估权衡论证时如果利用这一图解，当他对某个理由(无论正面还是反面)的真实性或可接受性提出质疑，就可以在对应的数字圆圈上标注“×”；若对某个理由与结论的相关性提出质疑，则可以在联结该理由与结论的直线或波浪箭头上标注“×”；若对OBC提出质疑，则可在表示PC“推倒”CC的线段上标注“×”。图11就清晰而直观地显示了评估者对正面理由①的真实性或可接受性、正面理由③对结论⑥的相关性，以及OBC的真实性所提出的质疑。

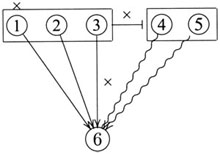
　　 图11

　　 6 结论

　　 通过批判性考察韦尔曼、希契柯克、戈维尔、汉森和弗里曼等学者在把握与图解权衡论证的结构诸问题上的所见所蔽，本文对这种同时包含正、反两面理由的独特论证的结构与图解展开了进一步的研究，认为反面理由是论证的一个非基本的构成要素，主张权衡论证具有一种由收敛和组合混合而成的双层结构，并在戈维尔原有方法的基础上引进了一种新方法对权衡论证给予更为充分的图解。

　　 *致谢：感谢加拿大温莎大学修辞、论证与推理研究中心布莱尔(J.Anthony Blair)和约翰逊(Ralph H.Johnson)教授对本文的一个早期英文版本[20]的写作帮助，以及美国纽约城市大学弗里曼(James B.Freeman)，加拿大莱斯布里奇大学戈维尔(Trudy Govier)、麦克马斯特大学希契柯克(David Hitchcock)和温莎大学品托(Robert C.Pinto)教授对该版本的评论与建议；感谢中山大学逻辑与认知研究所谢耘博士对本文写作的帮助。

　　 收稿日期：2016-06-20；修订日期：2016-07-05

　　 注释：

　　 ①“conductive argument”一词目前尚未有统一的译名，武宏志等将其译作“引导论证”([31]，第357页)，谢耘则称其为“联导性论证”([32]，第103页)。按韦尔曼对conductive reasoning的说明，“这种推理的特点就在于若干个理由联合导出(the leading together of various considerations)，故将其称作‘联导’(conduction)是恰当的。”([29]，第51页)据此，我对谢耘的译法略作修改，将此种论证称作“联导论证”。

　　 ②韦尔曼所说的联导(conduction)是一种既非演绎(deduction)亦非归纳(induction)的推理/论证。根据他的解释，演绎的特点在于结论从前提中必然得出，归纳指的是一个假说经由确立其蕴涵的真或假而得到确证或否证，联导则是“关于某一个案的结论，以并非毋庸置疑的方式(non-conclusively)从一个或多个关于同一个案的前提得出，而不诉诸任何其他的案例。”([29]，第52页)1980年，戈维尔率先将韦尔曼的这一思想引入非形式逻辑学界[9]，并在接下来的20余年里对其给予了持续的关注和扩展性的研究[10-12]。此外，希契柯克也发表了若干相关的研究成果[15-17]。2010年5月，来自加拿大、美国、德国、丹麦、瑞典和中国的10余位学者在加拿大温莎大学修辞、论证与推理研究中心召开了一次关于联导论证的小型国际研讨会，议题涉及联导论证的本质、合法性、类型、结构及其图解、评估，以及有关联导论证的历史渊源、个案研究等。提交此次研讨会的论文经过修改、扩充最后结集为《联导论证：一类被忽视的可废止推理》[4]。最近几年，围绕联导论证的本质与合法性等议题，坡辛(Kevin Possin,[24])、阿德勒(Jonathan Adler,[1])、布莱尔[2,3]、谢耘与熊明辉[30]等仍有研究与论辩。

　　 ③在韦尔曼那里，指称反面理由的语词有“negative consideration”、“reason against the conclusion”等，但戈维尔所用的“counter-consideration”一词在非形式逻辑领域更为通行。

　　 ④有必要指出的是，本文在分析权衡论证的各种实例时，仅仅是强调这些实例属于权衡论证的范畴，并不涉及对这些实例的评估，即不预设这些实例都是好的权衡论证。

　　 ⑤戈维尔的《论证的实践研究》是一本具有广泛影响的、体现了非形式逻辑理念的导论性质逻辑教材。自1985年首版以来，不断修订再版。本文引用的是该教材2010年出版的第7版。

　　 ⑥希契柯克曾提出，如果把premise(前提)追溯到亚里士多德所使用的protasis一词，那么“前提就是论证由其出发的东西(that from which an argument starts)”，而无论是支持结论的理由还是反对结论的理由，均可作为论证由其出发的起点([18]，第71页)。或许正是基于这种理解，他认为反面理由可叫作“否定相关的前提”(negatively relevant premise)或“反面前提”(con premise)，通常意义上的前提则可称为“肯定相关的前提”(positively relevant premise)或“正面前提”(pro premise)。[17]在[20]的第26页，我曾认为希契柯克的这一做法也是处理反面理由地位问题的一种办法，不过考虑到保持“前提”一词在逻辑学中的通常含义的优先性，我不再坚持上述看法。

　　 ⑦约翰逊(Ralph H.Johnson)在[21]和[22]中提出反对意见(objection)是构成论证之论辩性外层(dialectical tier)的主要内容之一。在讨论反面理由的性质及其在论证中地位时，戈维尔有时认为反面理由与反对意见并不是一回事([11]，第229-231页)，有时又将二者等同起来([12]，第370页)。对于反面理由与反对意见之间的区别，进一步的讨论可以参见[23]和[20]。

　　 ⑧需要注意的是，当PC或CC仅包含一个理由时，这种存在于若干个理由与K之间的收敛结构将不复存在。

　　 ⑨对希契柯克、戈维尔有关权衡论证之结构的论述的分析、关于权衡论证具有一种由收敛与组合混合而成的双层结构的提法，一个较早的版本可以参见[20]。戈维尔后来接受了汉森([14]，第38-42页)和我对她的批评，修正了原有的关于权衡论证之结构的提法，表述了一种类似于我所提议的双层混合结构的观点：“当我们考虑肯定或否定相关的因素如何支持或反对结论时，存在着一个收敛(convergence)；当我们把这些因素和理由合计起来，并在推理中利用一些因素胜过其他因素这一判断来得出结论时，存在着一个组合(linkage)。”([13]，第273页)

　　 ⑩斯克里文(M.Striven)在[25]的第42页采用类似的方法对包含反面理由的平衡考虑论证进行了图解。

　　 (11)尽管没有使用“权衡论证”或“联导论证”之名，托马斯(Stephen N.Thomas)在[26]的第163-164页中也使用了一种类似的方法来图解“所有理由，正面的和反面的，与一个选择之间的相关性”。相异于戈维尔用波浪箭头来连接反面理由与结论，托马斯采用的是虚线。

　　 (12)需要指出的是，同样主张权衡论证具有一种由收敛与组合混合而成的双层结构，我和戈维尔对宏观层面的组合结构的理解并不完全相同。她主张这种组合结构存在于PC、CC、OBP和K之间，而我认为与其说OBP是这个组合结构的要素之一，还不如说这个组合结构通过OBP体现出来。后文有进一步的讨论。

　　 (13)关于刻画论证结构的过程视角与结果视角，进一步的讨论可以参见[7]和[28]。

【参考文献】

[1]J.E.Adler,2013,"Are conductive arguments possible?",Argumentation,27:245-257.

[2]J.A.Blair,2013,"Are conductive arguments really not possible?",in D.Mohammed and M. (eds.),Virtues of Argumentation:Proceedings of the 10th International Conference of the Ontario Society for the Study of Argumentation,pp.1-13,Windsor,ON:OSSA.

[3]J.A.Blair,2016,"A defense of conduction:A reply to Adler",Argumentation,30:109-128.

[4]J.A.Blair and R.H.Johnson(eds.),2011,Conductive Argument:An Overlooked Type of Defeasible Reasoning,London:College Publications.

[5]I.M.Copi et al.,2011,Introduction to Logic(14th edition),New York:Pearson Education.

[6]J.B.Freeman,1991,Dialectics and the Macrostructure of Arguments:A Theory of Argument Structure,New York:Foils Publications.

[7]J.B.Freeman,2011,Argument Structure:Representation and Theory,Dordrecht:Springer Science+Business Media.

[8]J.B.Freeman,2011,"Evaluating conductive arguments in light of the Toulmin model",in J.A.Blair and R.H.Johnson(eds.),Conductive Argument:An Overlooked Types of Defeasible Reasoning,pp.127-144,London:College Publications.

[9]T.Govier,1980,"Challenge and response by Carl Wellman",Informal Logic Newsletter,2:10-15.

[10]T.Govier,1987,Problems in Argument Analysis and Evaluation,Dordrecht:Foris Publications.

[11]T.Govier,1999,The Philosophy of Argument,Newport News,VA:Vale Press.

[12]T.Govier,2010,A Practical Study of Argument(7th edition),Belmont,CA:Wadsworth,Cengage Learning.

[13]T.Govier,2011,"Conductive argument:Overview of the symposium",in J.A.Blair and R.H.Johnson(eds.),Conductive Argument:An Overlooked Types of Defeasible Reasoning,pp.262-276,London:College Publications.

[14]H.V.Hansen,2011,"Notes on balance-of-considerations arguments",in J.A.Blair and R.H.Johnson(eds.),Conductive Argument:An Overlooked Types of Defeasible Reasoning,pp.31-51,London:College Publications.

[15]D.Hitchcock,1981,"Deduction,induction and conduction",Informal Logic Newsletter,3:7-15.

[16]D.Hitchcock,1983,Critical Thinking:A Guide to Evaluate Information,Agincourt:Methuen Publications.

[17]D.Hitchcock,1994,"Walidity in conductive arguments",in R.H.Johnson and J.A.Blair(eds.),New Essays in Informal Logic,pp.58-66,Windsor,ON:Informal Logic.

[18]D.Hitchcock,2003,"Toulmin's warrants",in F.H.van Eemeren et al.(eds.),Anyone Who Has a View:Theoretical Contributions to the Study of Argumentation,pp.69-82,Dordrecht:Kluwer Academic Publishers.

[19]P.J.Hurley,2012,A Concise Introduction to Logic(11th edition),Belmont,CA:Wadsworth,Cengage Learning.

[20]R.Jin,2011,"The structure of pro and con argument:A survey of the theories",in J.A.Blair and R.H.Johnson(eds.),Conductive Argument:An Overlooked Types of Defeasible Reasoning,pp.10-30,London:College Publications.

[21]R.H.Johnson,2OOO,Manifest Rationality:A Pragmatic Theory of Argument,Mahwah,NJ:Erlbaum.

[22]R.H.Johnson,2002,"Manifest rationality reconsidered:Reply to my fellow symposiasts",Argumentation,16:311-331.

[23]R.H.Johnson,2011,"The relationship between pro/con and dialectical tier arguments",in J.A.Blair and R.H.Johnson(eds.),Conductive Argument:An Overlooked Types of Defeasible Reasoning,pp.52-61,London:College Publications.

[24]W.Possin,2012,"The myth of conductive arguments",Inquiry:Critical Thinking across the Disciplines,25:29-33.

[25]M.Scriven,1976,Reasoning,New York:McGraw-Hill Book Company.

[26]S.N.Thomas,1973,Practical Reasoning in Natural Language(1st edition),Englewood Cliffs,NJ:Prentice-Hall.

[27]S.E.Toulmin,2003,The Uses of Argument(updated edition),Cambridge:Cambridge University Press.

[28]D.Walton,1996,Argument Structure:A Pragmatic Theory,Toronto,ON:University of Toronto Press.

[29]C.Wellman,1971,Challenge and Response:Justification in Ethics,Carbondale,IL:Southern Illinois University Press.

[30]Y.Xie and M.Xiong,2013,"Commentary on:J.Anthony Blair's 'are conductive arguments really not possible?'",in D.Mohammed and M. (eds.),Virtues of Argumentation:Proceedings of the 10th International Conference of the Ontario Society for the Study of Argumentation,pp.1-6,Windsor,ON:OSSA.

[31]武宏志、周建武、唐坚，非形式逻辑导论，2009年，北京：人民出版社。

（原载《逻辑学研究》(广州)2016年第20163期）